系統中的大多數文件有多大？

你覺得，你的系統中大多數文件大概有多大？

這是一個很有意思的問題，你可以試着先猜一下。

基於對系統中保存文件的瞭解，可能有這樣的思考過程：

• 我收藏了好多照片，每個有 2~5MiB 吧。
• 我下載了好多漫畫，每個 100KiB 左右，這些大概佔了不少比例。
• 我還收藏了不少動畫電影電視劇，雖然這些文件總數量可能不多？
• 我下載了 Linux 的源碼，那裏面每個 C 代碼文件都幾千行，每行 100 字寬，平均也得有 30KiB 吧，有幾萬個源碼文件呢，佔比應該挺大的……

問題中「大多數」其實是個挺不精確的稱呼，換個精確點的問法：你覺得你的系統中 文件大小的中位數 大概在什麼範圍內？或者說，文件系統中 文件大小的分佈情況 一般是怎樣的曲線？

這個問題其實還有多種別的問法，比如：一個常見的桌面或者服務器系統中，多大的文件算大文件， 多小的文件算小文件，什麼範圍內的大小算是普通呢？

經歷過基本的科學教育的人，大概會做這樣的基於科學假設的猜測：

• 統計學上說，大量獨立隨機事件的累積概率滿足正態分佈（常態分佈）曲線。假設我們把某個特定文件的大小增長 1字節看作是一次獨立隨機事件，那麼文件大小在文件系統中應該是滿足正態分佈的？
• 正態分佈的前提下，平均數接近中位數，文件系統的已佔用大小除以文件數量大概就是大部分文件的大小了吧。
• 根據我現在文件系統的佔用大小和文件數量，平均數大概是 500KiB 左右？
• 雖然我還存了幾個非常大，上 GiB 的文件，但是看起來似乎也有很多很多非常小的文件， 平均一下的話應該會把平均數拉大，大於中位數吧。那麼中位數應該在 100KiB 這樣的量級附近？

你說爲什麼要關心這個？因爲我經常在網上看到這樣的討論：

「我有個倉庫盤要存很多下載到的漫畫，每個漫畫都是一個文件夾裏面一堆 小 JPG ，每個就幾十 KiB 。網上看到的說法是 XFS 對 小文件 的性能不那麼好，我是不是該換 EXT4 ？我還想在 Windows 上能讀寫，是不是 ExFAT 這種簡單的文件系統更合適一點？」

「軟件源的鏡像服務器需要存的都是些 小文件 吧，大多數軟件包壓縮後也就是幾個 KiB 到幾個 MiB 的量級，這種需求是不是適合用對 小文件 優化比較好的文件系統？」

「我的程序需要分析的數據是大量幾百K的 小文件 ，該怎麼存合適呢，直接用文件系統還是應該上數據庫？ 我還想多線程併發分析，是不是 SQL 數據庫的併發能力強一些？又或者 MongoDB 的 GridFS 看起來似乎能結合文件系統和數據庫的特點，選它應該還不錯？」

有沒有覺得上面這些討論和直覺有些出入？如果你的直覺告訴你，上面的討論似乎很自然的話， 那說明你需要繼續看下去了。

好了寫了這麼多廢話給大家思考時間，現在請回答一下我標題中那個問題， 你覺得，你的系統中大多數文件大概有多大？ ，接下來我要揭曉答案了。

統計實際系統中文件大小的學術研究

最近看到一個挺早以前的研究報告，是 FAST'11 的最優秀論文獎，研究的課題叫 《A Study of Practical Deduplication》 。這個研究原本是想考察一下在桌面文件系統中「去重」（deduplication）的可行性和潛在收益，作爲背景調查， 他們收集了一個挺大的調查樣本，記錄文件大小和校驗和之類的。從論文摘要看，他們在微軟公司內， 通過郵件的形式讓微軟員工在各自的工作機上執行他們的調查程序，大概在1個月左右的時間內收集到了 857 份調查結果。關於去重的研究結果這裏我們這裏先不深究，只看這個背景調查，他們對收集到的文件大小畫了個圖表：

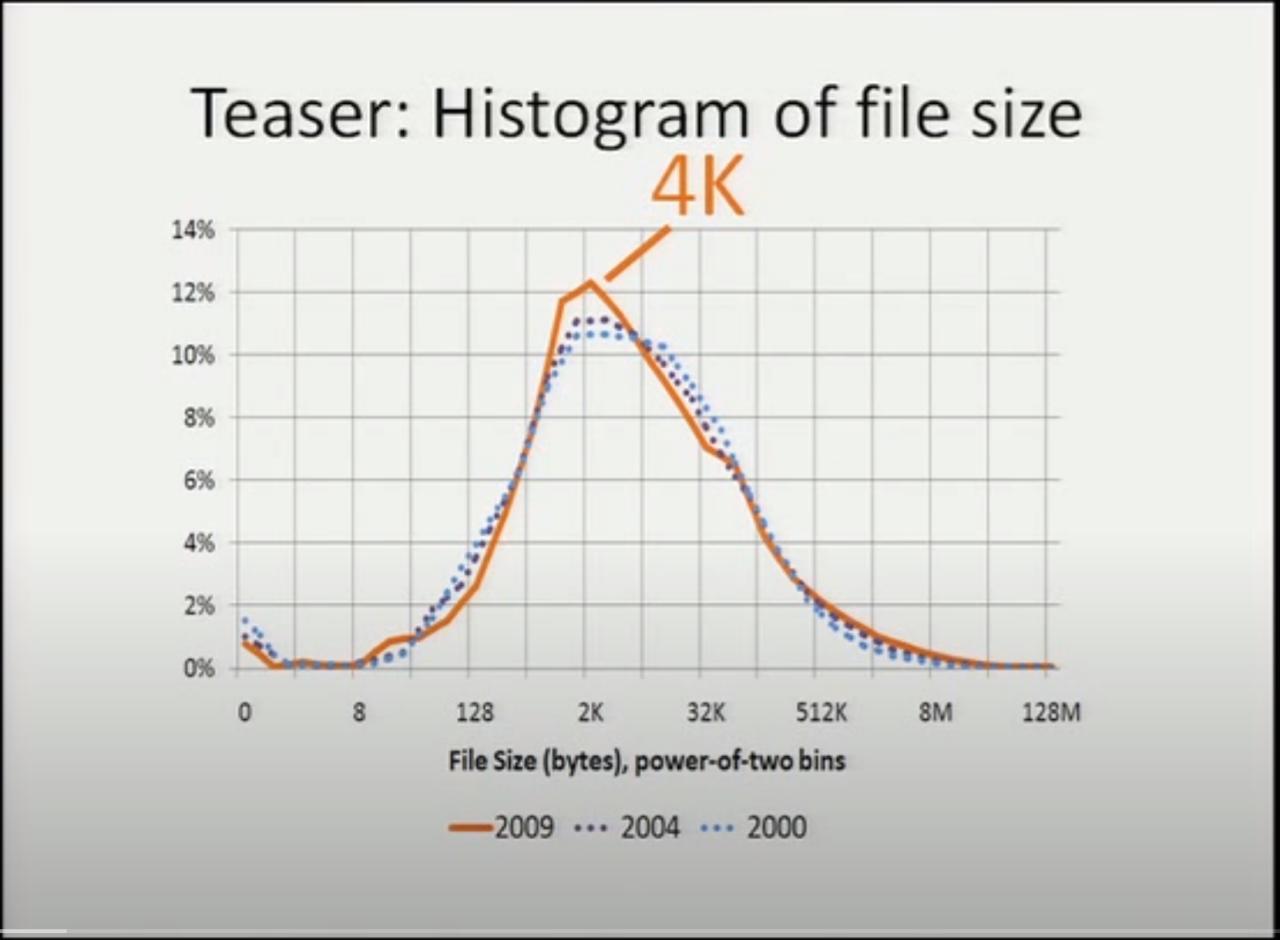
他們結果顯示最常見的文件大小是 4K ！

注意上圖裏的橫軸座標，是按2的指數來給文件大小分類的。比如 128~256 字節的算一類， 4K~8K 字節的算一類，分類之後統計每一類裏面文件的數量所佔比例，也就是說橫軸座標是指數增長的。 在指數增長的橫軸座標上，畫出的曲線才看起來像是正態分佈的曲線，如果把橫軸座標畫成線性的話， 中位數會出現在非常靠近左側小文件的地方。

也就是說根據他們的統計，文件系統中大部分文件都是大概 2K 到 8K 這樣的範圍，最常見 4K 大小。 非常大的比如 8M 以上的文件只是極個別，位於圖表右側非常長的尾巴中。

其實我對這個結果還不是很驚訝，因爲我記得在 2000 年左右，當我家的電腦還在用 Windows 98 跑在 40G 的 FAT32 文件系統中的時候，讀到過一篇介紹 NTFS 的「新」特性的文章。那篇文章講到 FAT32 的簇大小隨着分區大小增長，越來越大的簇大小對保存大量小文件極其浪費，而 NTFS 用固定的 4K 簇大小可避免這樣的浪費，並且 1K MFT 記錄甚至能「內聯（inline）」存儲非常小的文件。 爲了證明大量小文件對文件系統是個現實存在的問題，那篇文章也提到了常見系統中的文件大小分佈曲線， 提到了大部分文件都是 4K 大小這有點反直覺的結論。

這次這個研究讓我覺得吃驚的是，文件大小分佈並沒有隨着硬盤大小的增加而增加，穩定在了 4K 這個數字上。 他們以前還進行過兩次類似的統計，分別在 2000 年和 2004 年，圖中的點線畫出了歷史上的統計分佈，實線是 2009 年的最新統計。三年獲得的統計結果的曲線基本吻合，這意味着隨着存儲容量增長，文件大小的分佈幾乎沒有變化。

正當我疑惑，這種文件大小不變的趨勢，是否是因爲微軟公司內特定的操作系統和工作內容， 在別的系統上或者在更長的時間跨度上是否有類似的趨勢呢？這時演講的幻燈片翻了一頁：

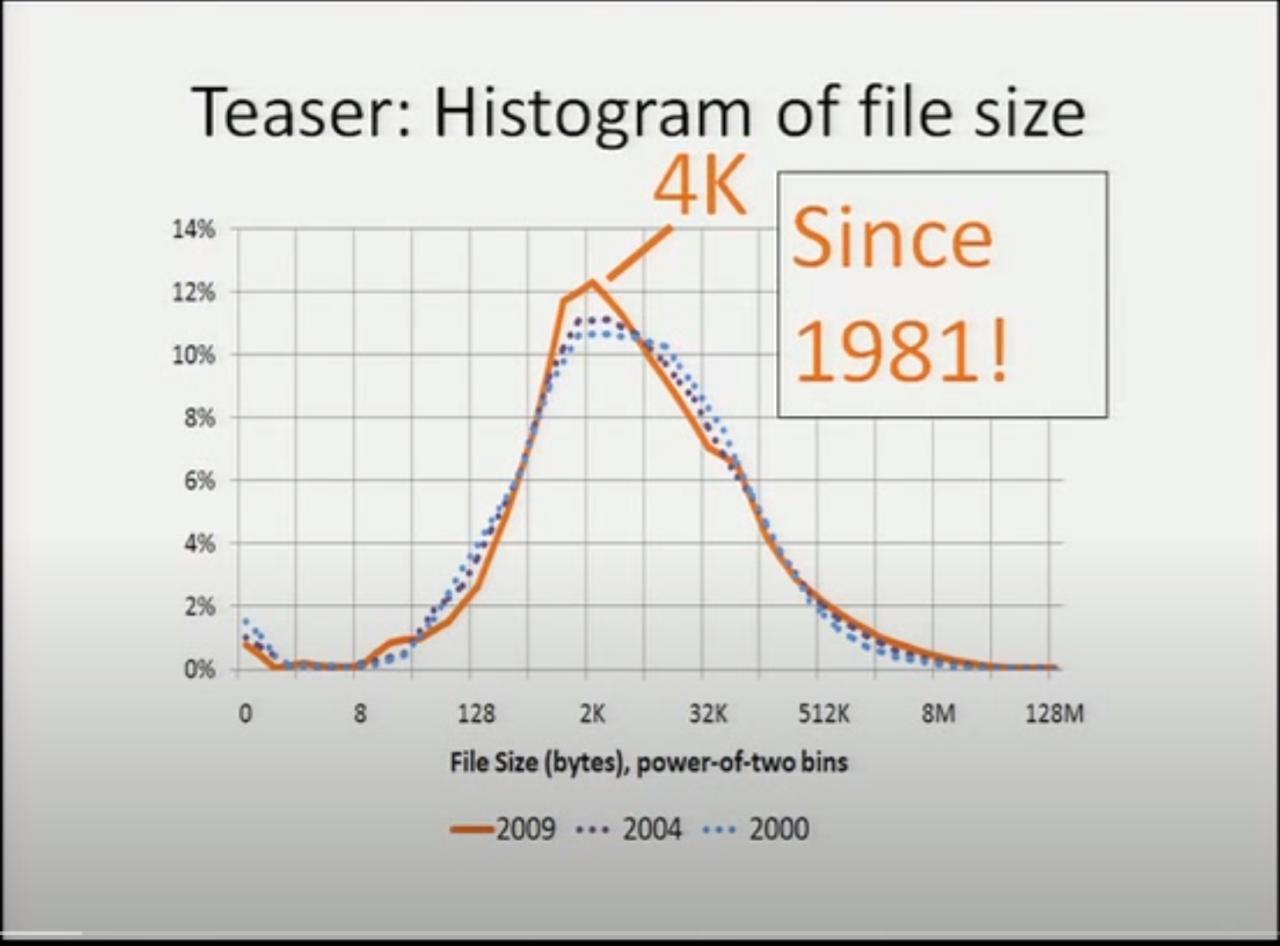
從早在 1981 年起，有研究表明文件系統中文件大小中位數就穩定在了 4K ！

在他們論文的參考文獻中，能找到 這個 1981 年的研究 。這篇早年的調查是在 DEC 的 PDP-10 機器上，使用 TOPS-10 操作系統。從現在的視點來看，被調查的 TOPS-10 的文件系統已經可以說非常初級了，沒法支持很大的文件或者很多的文件， 然而即便如此常見文件大小也還是非常符合現代系統中得到的結果。

微軟的研究者們還回顧了計算機科學領域多年的相關研究，結論是常見文件大小這個值在 1981 到 2009 這近 30 年中都非常穩定。演講的原文中這麼評價：

…… the median file size is 4k. It was 4k the other two years of the study. We've actually gone back through the literature. It turns out it's 4k in every study going back to the last 30 years. So this is great news. We can finally compete with physicists: we have our own fundamental constant of the universe, it's a medium file size ……

文件大小中位數是 4K 。在前幾年的兩次研究中它也是 4K 。其實我們回顧了既往的學術研究，發現在過去30 年中每個研究都說它是 4K 這個值。這是個好消息，我們終於有了一個堪比物理學家的結論：我們有我們自己的 宇宙基本常數了，是文件大小中位數。

這個結論很有意思，文件大小中位數在計算機科學領域的穩定程度堪比宇宙基本常數： 4K ！

很明顯這是在調侃，文件大小這種變化很大的數字顯然和文件系統內存儲的內容直接相關， 存遊戲的可能不同於存音樂的。但是這調侃的背後也有一定真實性：文件系統中保存的文件， 除了用戶直接使用的那些視頻、文檔、代碼，還有大量文件是程序內部創建使用的，比如瀏覽器的緩存和 cookie ，這類不被用戶知曉的文件可能在數量上反而佔據絕大多數。 於是從文件系統這邊來看，大多數文件都是在 4K 左右的數量級，更大的文件是少數。

不信？你可以測一下自己的文件系統

我也想測一下我的文件系統中文件大小的分佈情況，於是稍微寫了點代碼測量和畫圖。如果你也想知道你的系統中 文件大小的分佈，那麼可以像我這樣測。

首先用 find 命令統計一下每個文件的大小，輸出到一個文件裏：

find /home -type f -printf "%s %p\n" > myhome.txt

上述命令對 /​home 中的所有普通文件而忽略文件夾和符號鏈接之類的（ -type f ），輸出文件大小字節數和文件路徑（ -printf "%s %p\n" ）。 如果文件名路徑中有特殊符號可能之後比較難處理，那麼可以 -printf "%s\n" 忽略路徑。

然後用 Python 的 Matplotlib 和 NumPy 對收集到的文件大小數據畫個直方圖（histogram）。 以下 filesizehistogram.py 腳本在這兒 能下載到。

#!/usr/bin/python3
import argparse
import matplotlib.pyplot as plt
import numpy as np
import sys
from math import *
from bisect import bisect_left


def numfmt(s):
    marks = "KMGTP"
    m = 0
    f = type(s) is float
    while s >= 1024 and m < len(marks):
        if f:
            s /= 1024.0
        else:
            s //=1024
        m += 1
    if f:
        return f"{s:.2f}{marks[m-1:m]}"
    else:
        return f"{s}{marks[m-1:m]}"

if __name__ == '__main__':
    parser = argparse.ArgumentParser(
        prog = "filesizehistogram",
        description = """
            can use "-" as input filename, indicate input is taken from stdin.
            otherwise input file should be a result of "find -printf \'%s %p\\n\'"
            """
    )
    parser.add_argument('-o', '--output', help="output filename, will recognize common extensions by matplot")
    parser.add_argument('input', nargs='+',  help="input filenames")
    args = parser.parse_args()

    filenames = [x if x != '-' else '/dev/stdin' for x in args.input]
    data=np.array([int(x.split(' ')[0]) for fn in filenames for x in open(fn)])
    mindatalog2 = 5 # cut from 32
    maxdatalog2 = min(ceil(log2(data.max())), 31) # cut at 1G and above
    # bins [0, 1, 32, 64, 128, 256, ... , 1G, 2G] , last bin is open range
    bins=[0,1,] + [2**x for x in range(mindatalog2, maxdatalog2 + 1)]

    median = float(np.median(data))
    mean = float(data.mean())
    bmedian = bisect_left(bins, median) - 1
    bmean = bisect_left(bins, mean) - 1
    files = len(data)
    total = data.sum()

    hist, bin_edges = np.histogram(data,bins)
    fig,ax = plt.subplots(figsize=(20,8))
    ax.bar(range(len(hist)), hist, width=0.9)
    ax.set_xticks([i for i in range(len(hist))])
    tickbar = "┊\n"
    ax.set_xticklabels([f'{tickbar*(i%3)}{numfmt(bins[i])}~{numfmt(bins[i+1])}' for i in range(len(hist)-1)] +
                    [f"{numfmt(bins[len(hist)-1])}~"])

    ax.axvline(bmean, color='k', linestyle='dashed', linewidth=1)
    ax.axvline(bmedian, color='r', linestyle='dashed', linewidth=2)
    min_ylim, max_ylim = plt.ylim()
    min_xlim, max_xlim = plt.xlim()
    ax.text(bmean + 0.5   , max_ylim * 0.9, f'Mean: {numfmt(mean)}')
    ax.text(bmedian + 0.5 , max_ylim * 0.9, f'Median: {numfmt(median)}', color='r')
    ax.text(max_xlim * 0.8, max_ylim * 0.9, f'Files: {files}')
    ax.text(max_xlim * 0.9, max_ylim * 0.9, f'Total: {numfmt(float(total))}')

    for i in range(len(hist)):
        ax.text(i - 0.5, hist[i] + files / 400, f"{hist[i]:5}") # label on top of every bar, uplefted a little

    if args.output:
        plt.savefig(args.output)
    else:
        plt.show()

然後就能 ./​filesizehistogram.py myhome.txt 這樣畫出一張圖。以下是我一臺機器上根目錄 /​ 和家目錄 /​home 放在一起的結果：

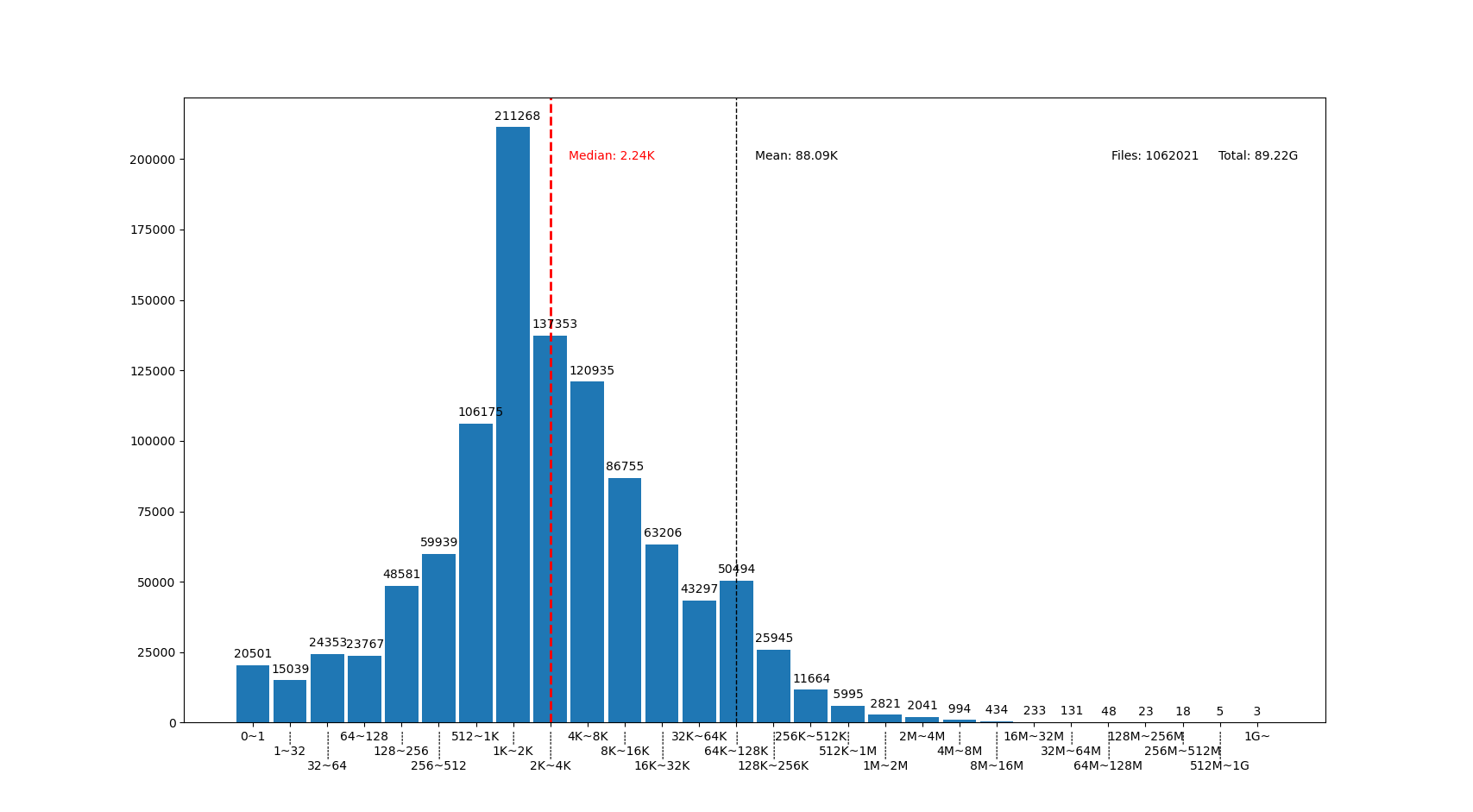
圖中我用點線標出了中位數（median）和平均數（mean）大小的位置，可見在我的文件系統中， 文件大小中位數在 2.24K ，平均數是 88.09K ，512~8K 範圍內的文件數量加在一起超過了文件總數一半。文件數量最多的範圍是 1K~2K ，大概因爲我家裏存了好多源代碼。還有一個小突起在 64K~128K ，這堆主要是我收藏的漫畫 JPG 文件。

圖的橫座標和上面微軟的研究類似，用2倍增長的bin統計文件數量。 不過稍微修改了一下，因爲我想知道 0 大小文件的個數，還想把 1~32 和 1G~ 以上這兩個曲線底端的尾巴放在一起統計。圖的縱座標是文件數。

也可以用這個來畫你感興趣的文件夾的文件大小分佈，比如用 linux 內核代碼樹畫出來的圖大概這樣：

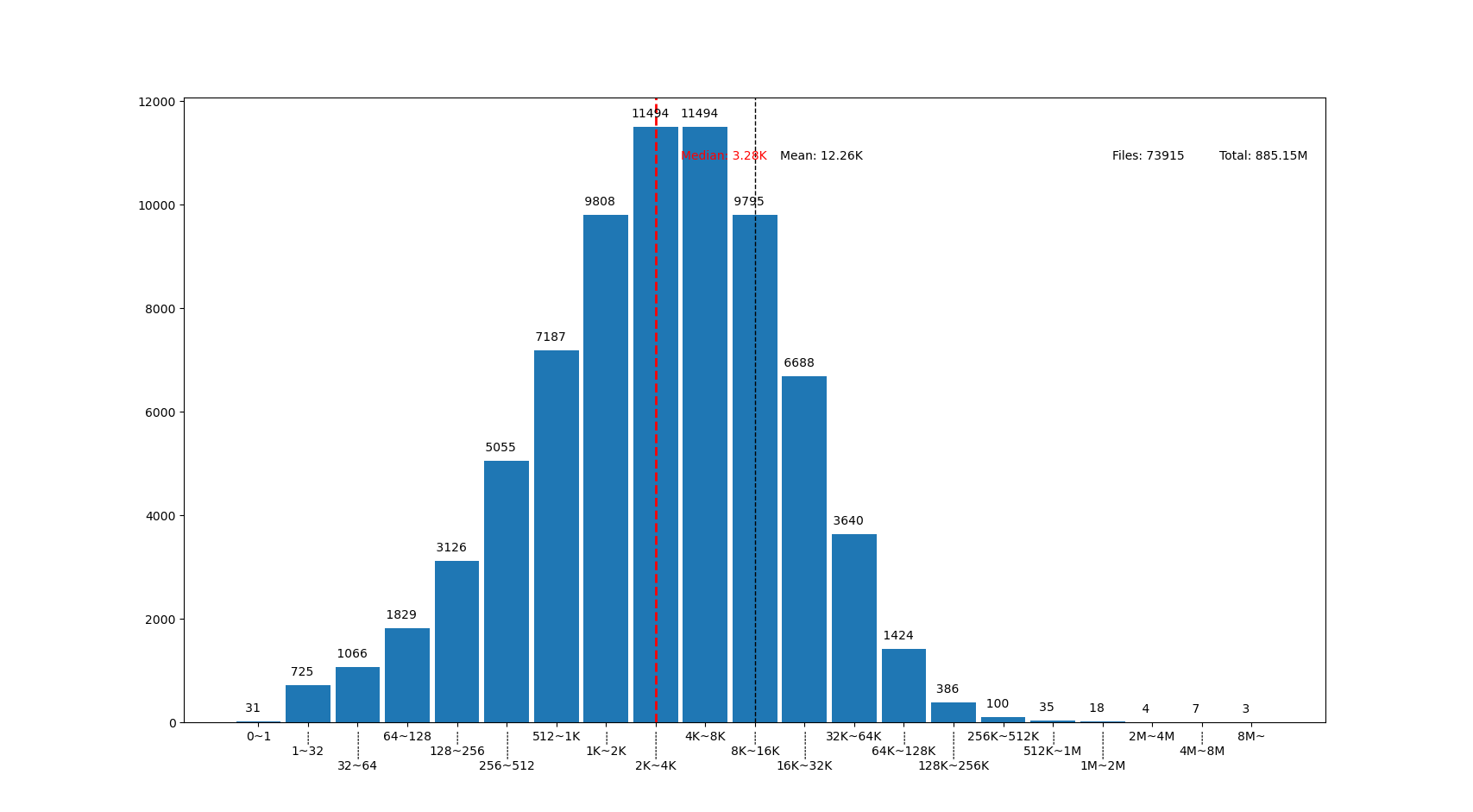
linux 代碼樹的文件大部分比我猜的 30K 要小呢，主要在 1K~16K ，中位數 3.28K 。而且意外得在代碼樹裏有好幾個 0 大小的文件，看了幾個文件路徑確認了一下，它們的確是 0 大小的頭文件，並不是我的文件系統丟了文件內容。

結論

有沒有覺得「文件大小的中位數是 4K 」這個結論出乎意料呢？

你在用的系統中文件大小的分佈曲線又是什麼樣的呢？歡迎留言告訴我。（貼圖可以用 https://fars.ee/f 圖牀呀）

知道了文件大小分佈的規律，就會發現設計文件系統的時候，需要考慮兩個極端情況： 既要照顧到文件系統中數量很少而大小超大的那些文件，又要考慮到這麼多數量衆多而大小只有數 K 的文件。也會發現，對於文件系統而言，超過 16K 的文件就絕不會被算作是「小文件」了，而文件系統設計中說的 「小文件優化」針對的通常是更小的文件大小。並且這一趨勢並不會隨着存儲設備容量增加而改變， 不能妄圖通過隨着容量逐步增加文件分配「簇」大小的方式，來簡化文件系統設計。

那麼衆多文件系統實際是如何滿足這些極端情況的呢？待我有空再細聊……