系统中的大多数文件有多大？

你觉得，你的系统中大多数文件大概有多大？

这是一个很有意思的问题，你可以试着先猜一下。

基于对系统中保存文件的了解，可能有这样的思考过程：

• 我收藏了好多照片，每个有 2~5MiB 吧。
• 我下载了好多漫画，每个 100KiB 左右，这些大概占了不少比例。
• 我还收藏了不少动画电影电视剧，虽然这些文件总数量可能不多？
• 我下载了 Linux 的源码，那里面每个 C 代码文件都几千行，每行 100 字宽，平均也得有 30KiB 吧，有几万个源码文件呢，占比应该挺大的……

问题中「大多数」其实是个挺不精确的称呼，换个精确点的问法：你觉得你的系统中 文件大小的中位数 大概在什么范围内？或者说，文件系统中 文件大小的分布情况 一般是怎样的曲线？

这个问题其实还有多种别的问法，比如：一个常见的桌面或者服务器系统中，多大的文件算大文件， 多小的文件算小文件，什么范围内的大小算是普通呢？

经历过基本的科学教育的人，大概会做这样的基于科学假设的猜测：

• 统计学上说，大量独立随机事件的累积概率满足正态分布（常态分布）曲线。假设我们把某个特定文件的大小增长 1字节看作是一次独立随机事件，那么文件大小在文件系统中应该是满足正态分布的？
• 正态分布的前提下，平均数接近中位数，文件系统的已占用大小除以文件数量大概就是大部分文件的大小了吧。
• 根据我现在文件系统的占用大小和文件数量，平均数大概是 500KiB 左右？
• 虽然我还存了几个非常大，上 GiB 的文件，但是看起来似乎也有很多很多非常小的文件， 平均一下的话应该会把平均数拉大，大于中位数吧。那么中位数应该在 100KiB 这样的量级附近？

你说为什么要关心这个？因为我经常在网上看到这样的讨论：

「我有个仓库盘要存很多下载到的漫画，每个漫画都是一个文件夹里面一堆 小 JPG ，每个就几十 KiB 。网上看到的说法是 XFS 对 小文件 的性能不那么好，我是不是该换 EXT4 ？我还想在 Windows 上能读写，是不是 ExFAT 这种简单的文件系统更合适一点？」

「软件源的镜像服务器需要存的都是些 小文件 吧，大多数软件包压缩后也就是几个 KiB 到几个 MiB 的量级，这种需求是不是适合用对 小文件 优化比较好的文件系统？」

「我的程序需要分析的数据是大量几百K的 小文件 ，该怎么存合适呢，直接用文件系统还是应该上数据库？ 我还想多线程并发分析，是不是 SQL 数据库的并发能力强一些？又或者 MongoDB 的 GridFS 看起来似乎能结合文件系统和数据库的特点，选它应该还不错？」

有没有觉得上面这些讨论和直觉有些出入？如果你的直觉告诉你，上面的讨论似乎很自然的话， 那说明你需要继续看下去了。

好了写了这么多废话给大家思考时间，现在请回答一下我标题中那个问题， 你觉得，你的系统中大多数文件大概有多大？ ，接下来我要揭晓答案了。

统计实际系统中文件大小的学术研究

最近看到一个挺早以前的研究报告，是 FAST'11 的最优秀论文奖，研究的课题叫 《A Study of Practical Deduplication》 。这个研究原本是想考察一下在桌面文件系统中「去重」（deduplication）的可行性和潜在收益，作为背景调查， 他们收集了一个挺大的调查样本，记录文件大小和校验和之类的。从论文摘要看，他们在微软公司内， 通过邮件的形式让微软员工在各自的工作机上执行他们的调查程序，大概在1个月左右的时间内收集到了 857 份调查结果。关于去重的研究结果这里我们这里先不深究，只看这个背景调查，他们对收集到的文件大小画了个图表：

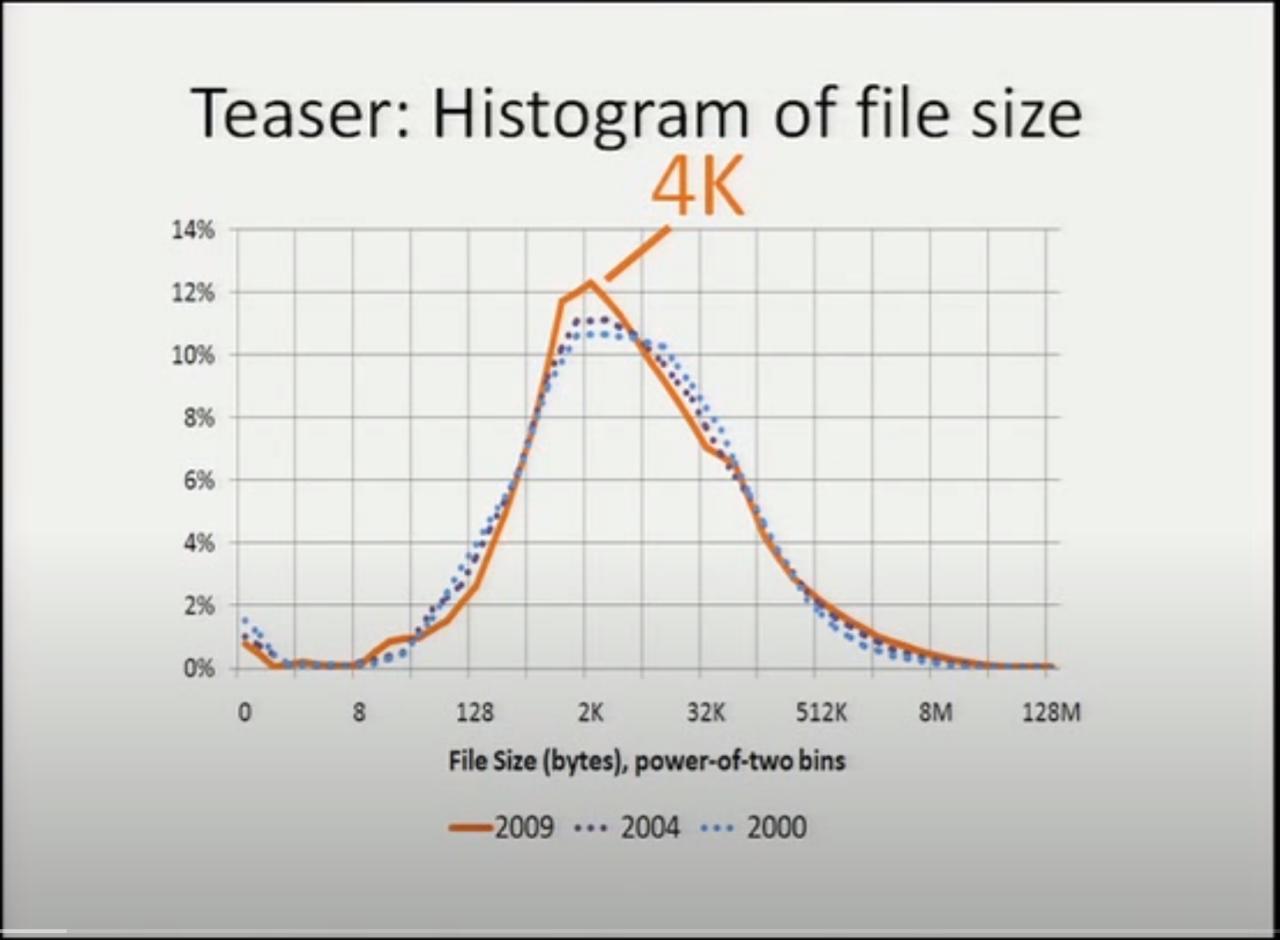
他们结果显示最常见的文件大小是 4K ！

注意上图里的横轴座标，是按2的指数来给文件大小分类的。比如 128~256 字节的算一类， 4K~8K 字节的算一类，分类之后统计每一类里面文件的数量所占比例，也就是说横轴座标是指数增长的。 在指数增长的横轴座标上，画出的曲线才看起来像是正态分布的曲线，如果把横轴座标画成线性的话， 中位数会出现在非常靠近左侧小文件的地方。

也就是说根据他们的统计，文件系统中大部分文件都是大概 2K 到 8K 这样的范围，最常见 4K 大小。 非常大的比如 8M 以上的文件只是极个别，位于图表右侧非常长的尾巴中。

其实我对这个结果还不是很惊讶，因为我记得在 2000 年左右，当我家的电脑还在用 Windows 98 跑在 40G 的 FAT32 文件系统中的时候，读到过一篇介绍 NTFS 的「新」特性的文章。那篇文章讲到 FAT32 的簇大小随着分区大小增长，越来越大的簇大小对保存大量小文件极其浪费，而 NTFS 用固定的 4K 簇大小可避免这样的浪费，并且 1K MFT 记录甚至能「内联（inline）」存储非常小的文件。 为了证明大量小文件对文件系统是个现实存在的问题，那篇文章也提到了常见系统中的文件大小分布曲线， 提到了大部分文件都是 4K 大小这有点反直觉的结论。

这次这个研究让我觉得吃惊的是，文件大小分布并没有随着硬盘大小的增加而增加，稳定在了 4K 这个数字上。 他们以前还进行过两次类似的统计，分别在 2000 年和 2004 年，图中的点线画出了历史上的统计分布，实线是 2009 年的最新统计。三年获得的统计结果的曲线基本吻合，这意味着随着存储容量增长，文件大小的分布几乎没有变化。

正当我疑惑，这种文件大小不变的趋势，是否是因为微软公司内特定的操作系统和工作内容， 在别的系统上或者在更长的时间跨度上是否有类似的趋势呢？这时演讲的幻灯片翻了一页：

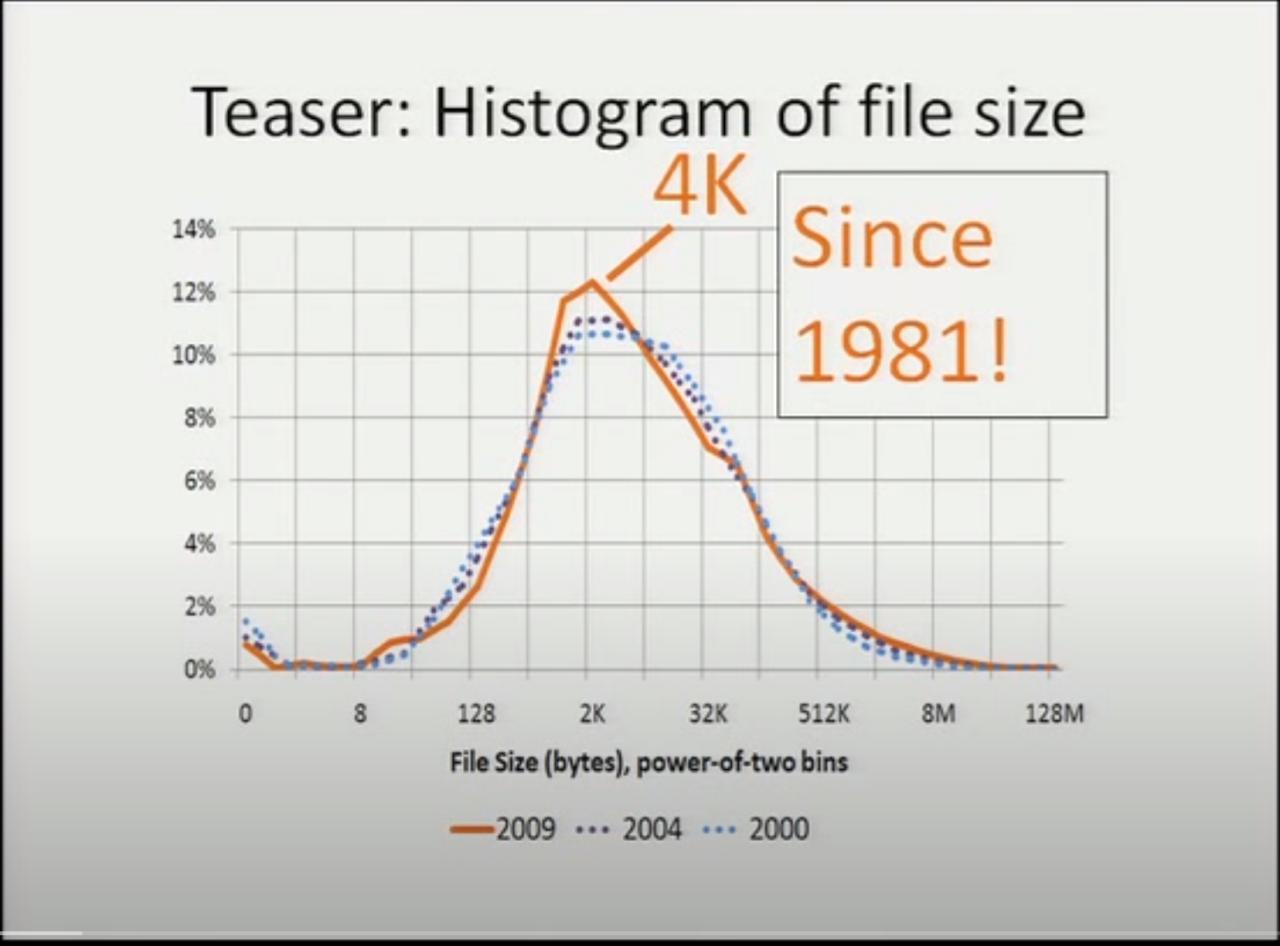
从早在 1981 年起，有研究表明文件系统中文件大小中位数就稳定在了 4K ！

在他们论文的参考文献中，能找到 这个 1981 年的研究 。这篇早年的调查是在 DEC 的 PDP-10 机器上，使用 TOPS-10 操作系统。从现在的视点来看，被调查的 TOPS-10 的文件系统已经可以说非常初级了，没法支持很大的文件或者很多的文件， 然而即便如此常见文件大小也还是非常符合现代系统中得到的结果。

微软的研究者们还回顾了计算机科学领域多年的相关研究，结论是常见文件大小这个值在 1981 到 2009 这近 30 年中都非常稳定。演讲的原文中这么评价：

…… the median file size is 4k. It was 4k the other two years of the study. We've actually gone back through the literature. It turns out it's 4k in every study going back to the last 30 years. So this is great news. We can finally compete with physicists: we have our own fundamental constant of the universe, it's a medium file size ……

文件大小中位数是 4K 。在前几年的两次研究中它也是 4K 。其实我们回顾了既往的学术研究，发现在过去30 年中每个研究都说它是 4K 这个值。这是个好消息，我们终于有了一个堪比物理学家的结论：我们有我们自己的 宇宙基本常数了，是文件大小中位数。

这个结论很有意思，文件大小中位数在计算机科学领域的稳定程度堪比宇宙基本常数： 4K ！

很明显这是在调侃，文件大小这种变化很大的数字显然和文件系统内存储的内容直接相关， 存游戏的可能不同于存音乐的。但是这调侃的背后也有一定真实性：文件系统中保存的文件， 除了用户直接使用的那些视频、文档、代码，还有大量文件是程序内部创建使用的，比如浏览器的缓存和 cookie ，这类不被用户知晓的文件可能在数量上反而占据绝大多数。 于是从文件系统这边来看，大多数文件都是在 4K 左右的数量级，更大的文件是少数。

不信？你可以测一下自己的文件系统

我也想测一下我的文件系统中文件大小的分布情况，于是稍微写了点代码测量和画图。如果你也想知道你的系统中 文件大小的分布，那么可以像我这样测。

首先用 find 命令统计一下每个文件的大小，输出到一个文件里：

find /home -type f -printf "%s %p\n" > myhome.txt

上述命令对 /​home 中的所有普通文件而忽略文件夹和符号链接之类的（ -type f ），输出文件大小字节数和文件路径（ -printf "%s %p\n" ）。 如果文件名路径中有特殊符号可能之后比较难处理，那么可以 -printf "%s\n" 忽略路径。

然后用 Python 的 Matplotlib 和 NumPy 对收集到的文件大小数据画个直方图（histogram）。 以下 filesizehistogram.py 脚本在这儿 能下载到。

#!/usr/bin/python3
import argparse
import matplotlib.pyplot as plt
import numpy as np
import sys
from math import *
from bisect import bisect_left


def numfmt(s):
    marks = "KMGTP"
    m = 0
    f = type(s) is float
    while s >= 1024 and m < len(marks):
        if f:
            s /= 1024.0
        else:
            s //=1024
        m += 1
    if f:
        return f"{s:.2f}{marks[m-1:m]}"
    else:
        return f"{s}{marks[m-1:m]}"

if __name__ == '__main__':
    parser = argparse.ArgumentParser(
        prog = "filesizehistogram",
        description = """
            can use "-" as input filename, indicate input is taken from stdin.
            otherwise input file should be a result of "find -printf \'%s %p\\n\'"
            """
    )
    parser.add_argument('-o', '--output', help="output filename, will recognize common extensions by matplot")
    parser.add_argument('input', nargs='+',  help="input filenames")
    args = parser.parse_args()

    filenames = [x if x != '-' else '/dev/stdin' for x in args.input]
    data=np.array([int(x.split(' ')[0]) for fn in filenames for x in open(fn)])
    mindatalog2 = 5 # cut from 32
    maxdatalog2 = min(ceil(log2(data.max())), 31) # cut at 1G and above
    # bins [0, 1, 32, 64, 128, 256, ... , 1G, 2G] , last bin is open range
    bins=[0,1,] + [2**x for x in range(mindatalog2, maxdatalog2 + 1)]

    median = float(np.median(data))
    mean = float(data.mean())
    bmedian = bisect_left(bins, median) - 1
    bmean = bisect_left(bins, mean) - 1
    files = len(data)
    total = data.sum()

    hist, bin_edges = np.histogram(data,bins)
    fig,ax = plt.subplots(figsize=(20,8))
    ax.bar(range(len(hist)), hist, width=0.9)
    ax.set_xticks([i for i in range(len(hist))])
    tickbar = "┊\n"
    ax.set_xticklabels([f'{tickbar*(i%3)}{numfmt(bins[i])}~{numfmt(bins[i+1])}' for i in range(len(hist)-1)] +
                    [f"{numfmt(bins[len(hist)-1])}~"])

    ax.axvline(bmean, color='k', linestyle='dashed', linewidth=1)
    ax.axvline(bmedian, color='r', linestyle='dashed', linewidth=2)
    min_ylim, max_ylim = plt.ylim()
    min_xlim, max_xlim = plt.xlim()
    ax.text(bmean + 0.5   , max_ylim * 0.9, f'Mean: {numfmt(mean)}')
    ax.text(bmedian + 0.5 , max_ylim * 0.9, f'Median: {numfmt(median)}', color='r')
    ax.text(max_xlim * 0.8, max_ylim * 0.9, f'Files: {files}')
    ax.text(max_xlim * 0.9, max_ylim * 0.9, f'Total: {numfmt(float(total))}')

    for i in range(len(hist)):
        ax.text(i - 0.5, hist[i] + files / 400, f"{hist[i]:5}") # label on top of every bar, uplefted a little

    if args.output:
        plt.savefig(args.output)
    else:
        plt.show()

然后就能 ./​filesizehistogram.py myhome.txt 这样画出一张图。以下是我一台机器上根目录 /​ 和家目录 /​home 放在一起的结果：

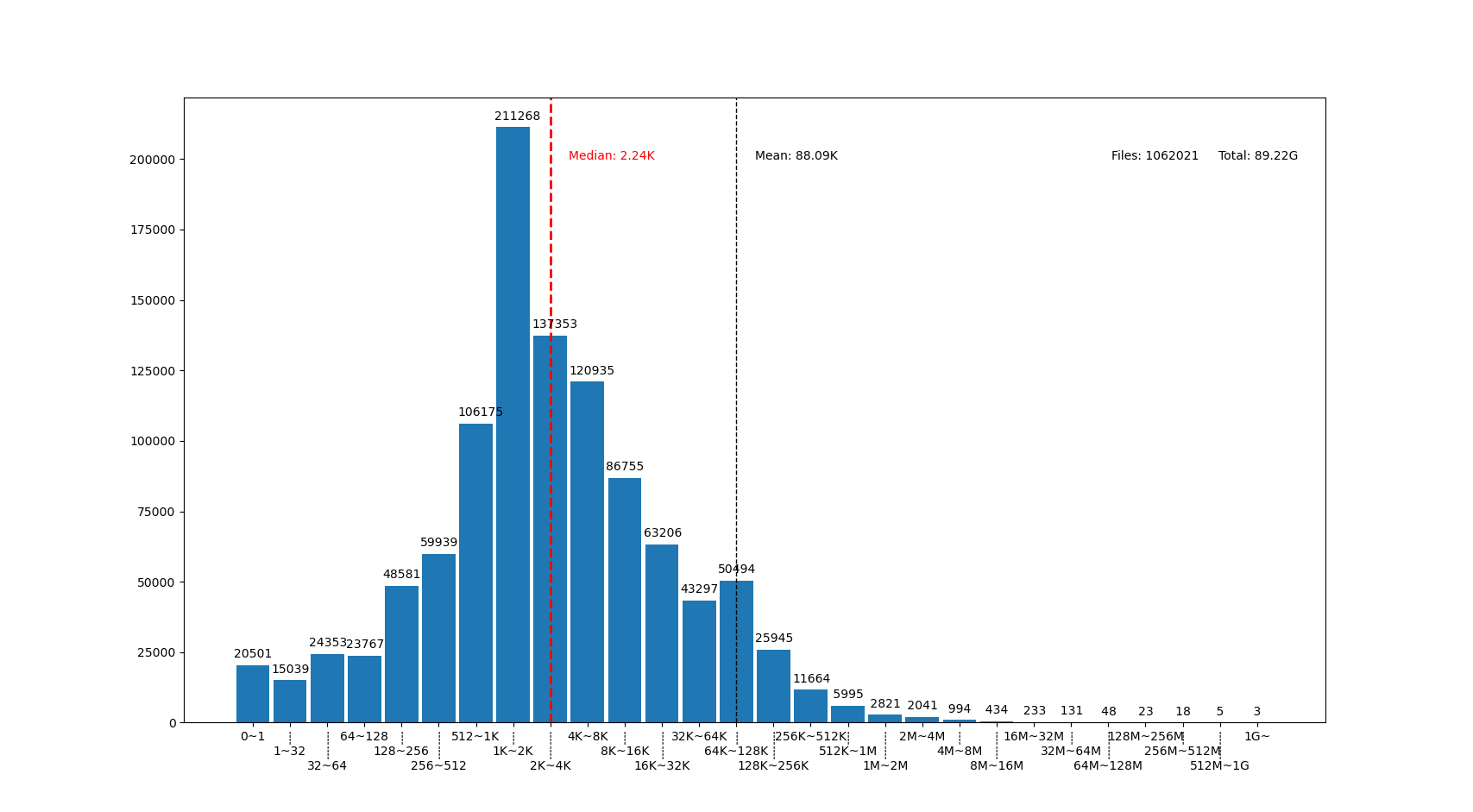
图中我用点线标出了中位数（median）和平均数（mean）大小的位置，可见在我的文件系统中， 文件大小中位数在 2.24K ，平均数是 88.09K ，512~8K 范围内的文件数量加在一起超过了文件总数一半。文件数量最多的范围是 1K~2K ，大概因为我家里存了好多源代码。还有一个小突起在 64K~128K ，这堆主要是我收藏的漫画 JPG 文件。

图的横座标和上面微软的研究类似，用2倍增长的bin统计文件数量。 不过稍微修改了一下，因为我想知道 0 大小文件的个数，还想把 1~32 和 1G~ 以上这两个曲线底端的尾巴放在一起统计。图的纵座标是文件数。

也可以用这个来画你感兴趣的文件夹的文件大小分布，比如用 linux 内核代码树画出来的图大概这样：

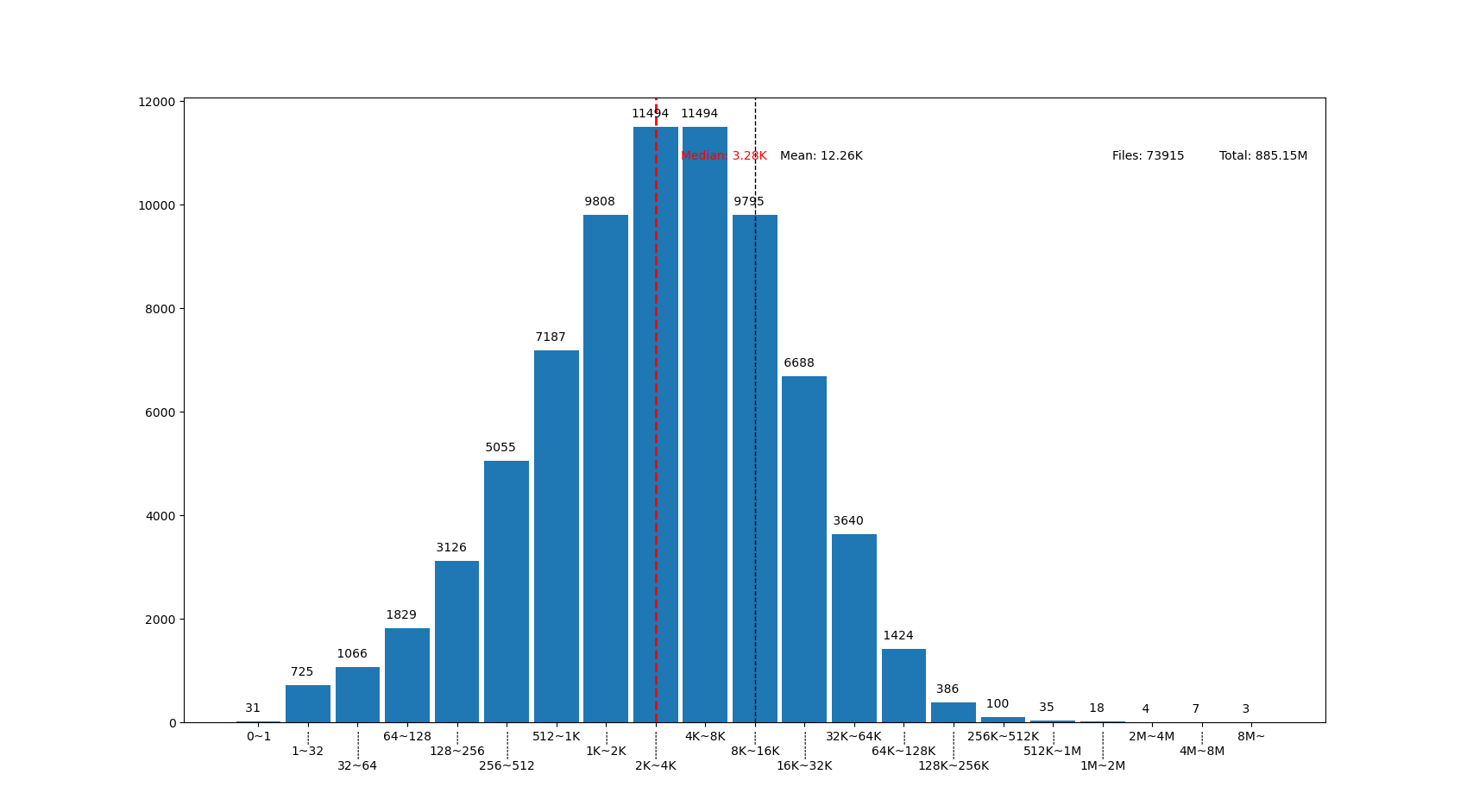
linux 代码树的文件大部分比我猜的 30K 要小呢，主要在 1K~16K ，中位数 3.28K 。而且意外得在代码树里有好几个 0 大小的文件，看了几个文件路径确认了一下，它们的确是 0 大小的头文件，并不是我的文件系统丢了文件内容。

结论

有没有觉得「文件大小的中位数是 4K 」这个结论出乎意料呢？

你在用的系统中文件大小的分布曲线又是什么样的呢？欢迎留言告诉我。（贴图可以用 https://fars.ee/f 图床呀）

知道了文件大小分布的规律，就会发现设计文件系统的时候，需要考虑两个极端情况： 既要照顾到文件系统中数量很少而大小超大的那些文件，又要考虑到这么多数量众多而大小只有数 K 的文件。也会发现，对于文件系统而言，超过 16K 的文件就绝不会被算作是「小文件」了，而文件系统设计中说的 「小文件优化」针对的通常是更小的文件大小。并且这一趋势并不会随着存储设备容量增加而改变， 不能妄图通过随着容量逐步增加文件分配「簇」大小的方式，来简化文件系统设计。

那么众多文件系统实际是如何满足这些极端情况的呢？待我有空再细聊……